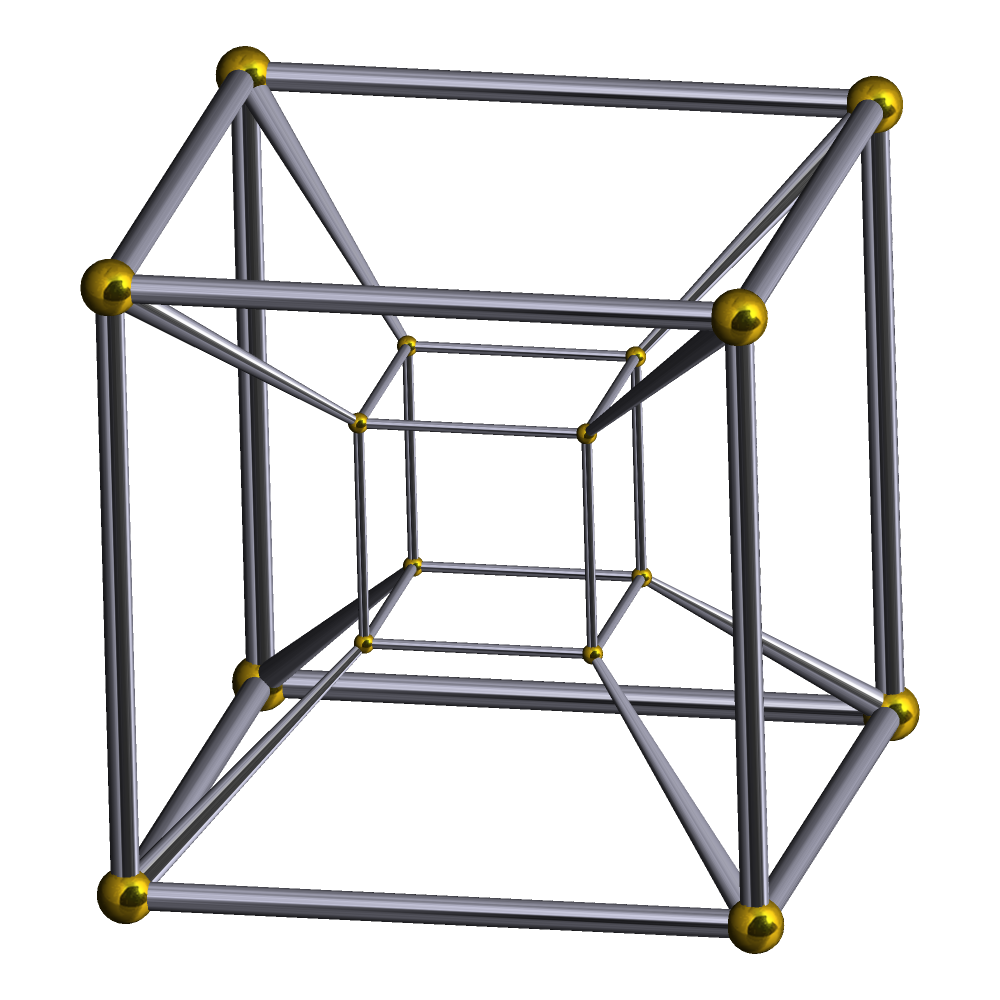
A tesseract, as everyone (or at least readers of Robert A. Heinlein)
knows, is a four dimensional cube or “hypercube”. Which means a
cube extended in a direction simultaneously perpendicular to all three
of its axes so that each cube of a tesseract shares a common side and
four common edges with each cube adjacent to it and with each cube
immediately adjacent to the adjacent cube.

Confused? Wondering what in the name of Anubis this has to do
with D&D and mapmaking? All will be made clear, at least as clear as is
necessary to make use of the idea — most Americans can’t completely
explain the internal combustion engine but we keep right on driving
cars anyway.

The tesseract is a mathematical abstraction whose math escapes
my high school algebra but whose properties are known and easily applied and adaptable to D&D. Look at figure 1. Bear in mind that each

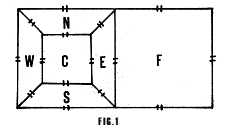
of the shapes shown is in fact a perfect square, which is meant to represent a floor plan of a cubical room. Therefore we have a central room
(C), an eastern room (E), a southern room (S), a western room (W), a
northern room (N), and another room we’ll call the frame room (F).
Not shown are the upper room (U) and lower room (L) which border
the top and bottom of the central room.

Rereading the first paragraph, we can see (that since E is adjacent
to C, it must share a wall with N and a wall with S. As represented, each
room does the same thing with adjacent rooms. Now for the real mindboggler: room F. F is adjacent to E; the rooms immediately adjacent to
E are N and S; therefore F shares a wall with N and a wall with S. But
sharing a wall makes the rooms adjacent, and W is adjacent to both N
and S, so F must share its fourth and final wall with W, which means
that room F is the room outside the square formed by the outer walls of
E, N, W, and S. . .

Never mind. For the purposes of the DM, all he need do is make
some such notation as exhibited in figure 2 and keep a separate map

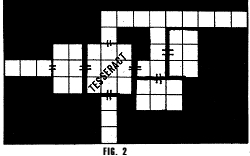
such as figure 3, which gives him the basic floor plan of his tesseract.
The arrows show the relationships of the walls well enough and still allow the DM to furnish the rooms in the proper dimensions. This floor
plan also shows the rooms directly above and below the central room,
to which some access should be planned. These two rooms present
some interesting problems I’ll elaborate later. For now, let’s look at
our basic plan. Suppose a party meanders down one of the corridors
shown in figure 2. After checking for traps, listening at the door, etc.
the party enters room C. (Room C is always the room which occupies
the square shown in figure 2.) So long as any door remains open, the
tesseract is not activated! ! ! Opening a second door will allow the party
to pass through room C as though the others didn’t exist. If, however,
all four doors are allowed to be closed at the same time, no matter how
briefly . . . thereafter all doors will lead to the next room of the tesseract.
Of course, some method should be provided for eventual escape —
a magical item, such as a ring or bracelet which will allow the wearer
and those around him to pass through one of the doors of room C into
the dungeon beyond. Such a device would be usable only in this tesseract, naturally. The crueller DM’s amongst us would no doubt leave out
such frills, forcing the hapless party to rely on teleport spells, wishes,
knock spells (if anyone would ever conceive of using one on a door
which opens easily — to another room that is), or even divine intervention. Note that a dispel1 magic spell would cause every room except C to
instantly disappear, along with anyone in them.

As previously mentioned, rooms U and L present peculiar problems. Looking at figure 4, a side view of your tesseract with ‘w’ meaning walls, ‘c’ for ceiling and ‘f’ for floors, an anomaly may become apparent; if one enters F by climbing through the ceiling of U, one finds
oneself climbing through the ceiling of F upside down! And of course
the corollary holds true for room L.
Unless you’re the type of DM who delights in having people fall on
their heads, it is highly recommended that you not bother to design in
an access between L or U and F. (Nor between L or U and any other

room except C, since L’s walls are E, N, W, and S’s floors, and U’s
walls are their ceilings.) The tesseract is complex enough without adding these unnecessary frills.
Now that the basics have been established, draw one up and play it
solo, populating it as your whims dictate, just to get the feel of it. Get
used to saying left and right instead of north, west, etc., since you’ve
seen that a straight line can take you in all four directions in a matter of
four rooms.

I first designed this fiendish set of rooms nearly a year ago, after a
close encounter with a member of that semi-intelligent species, papyriosus meticulosus, whose habits are well known; to wit, they must have
every detail of a dungeon set to parchment, every nook, crack, cranny,
or stain. I wasn’t the DM — I was one of the bored players whose time
he was wasting. After careful consultation, the DM included one in his
dungeon. I learned a valuable lesson — never call on Thor in a moment
of weakness — and the mapmaker should be out of the sanitarium early
next year. Good luck with your own mapmakers.

WHICH WAY IS UP?
WELL, IT ALL DEPENDS...

TESSERACTS
Allen Wells

 

-	-	-	-	-
Dragon 38	-	-	Best of Dragon, Vol. II	Dragon

I was recently reading some back issues of  The Dragon  when I
came across an interesting article about the use of Tesseracts in  D&D
(Tesseracts, TD #17, August 1978).  The article was very good, as far
as it went, but there are many more possibilities to be explored.
A fairly thorough description of a tesseract is necessary at first, for
readers to understand the rest of the article. If you think you already
understand tesseracts, you may just skim this section and look at the
diagrams.

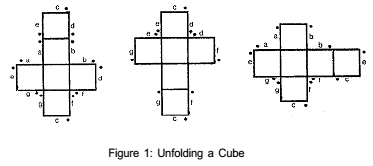
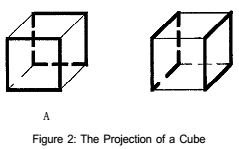
There are two ways of showing a cube in two dimensions. Unfolding the cube and showing how to put it back together again (fig
1), or showing what its ?projection? or ?shadow? into 2-space looks
like (fig 2). Similarly, there are two ways to show a tesseract in three
dimensions.

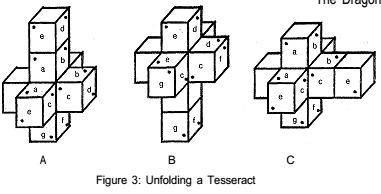
The first way to show a tesseract is to  ?unfold?  it. Compare figure
1 to figure 3. In figure 1 the two lines labelled ?a? connect to each
other in such a way that the dots connect. Note that 1A, 1B, and 1C
will all give you the same cube if you cut them out and fold them into
cubes. In figure 3, the two faces
of cubes labelled ?a? connect to
each other in such a way that
the dots connect. Since these
faces are really connected, you
can redraw the tesseract as in l
figure 3B where I have ?rolled?
the cubes up the tesseract. I
could have rolled them again
(?e? matches ?e? and ?d?
matches ?d?).

Now that we can see how
the ?d? faces match, I can move
the top cube to match the side
cube (transition from 3A to
3C). Note the orientation of
Now we can begin to explore the possibilities of a tesseract. Start
out by mapping out your dungeon, either using figure 3A  and
showing how all the faces connect, or 4A. In either case you have to
keep track of what cube you are mapping in and what surface is the
floor.

This brings up the first problem: Which way is down?? My answer
is,  down is the way your feet are pointing!!!  This doesn?t mean that if
you turn your feet, you turn ?down,? but when you open a door,
?down? will still be ?down? in the next room!  This means that gravity is
a property of you and your possessions, not of the room,  and it is
possible to have two people in the same room who think a different
?wall? is the ?floor.?

As an example, consider figure 3. Let us say that an intrepid
group of adventurers starts in the bottom cube in figure 3A. Athmar
goes upstairs into the cube in the center (which cannot be seen in the
diagram) and goes through a door toward us into the cube that has
faces ?a?, ?c? , and ?e? (the one poking out). He is now standing on face
?g? (see 3B). Mythner, who stayed behind in the ?bottom? cube,
the dot on face ?e?. So 3A, 3B,
and, 3C would all give you the
same tesseract if you could cut
them out and fold them into tesseracts. Try to imagine other ways
you could restructure the tesseract (Note: The top face of the top
cube and the bottom face of the bottom cube connect in figures 3A
and 3B.)

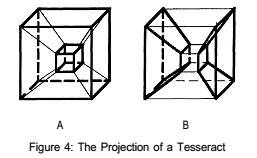
The other way to show a tesseract is to show its  ?projection?.
Compare figure 2 to figure 4. This projection shows the relation
between the cube faces better, but at the cost of distorting the cubes,
just like the projection shows the relation between the edges of a
cube better, but at the cost of distorting some of the faces. Figures 2A
and 4A have the non-distorted faces/cubes in bold. Figures 2B and
4B show some of the distorted faces/cubes. Note how the distorted
faces look like parallelograms and the distorted cubes look like
pyramids with the tops cut off.

Look at both of these representations and try to imagine moving
from one cube to another. Up does not always remain up! Some
people will find the unfolding more understandable, some the projection. Use whichever one you find easier.

decides to go adventuring on
his own into the same cube by
taking a door through face ?g?,
and is now standing on face ?e?.
Athmar and Mythner are in the
same room, but  they each
think that a different way is up!
This shows an interesting fact;
although there are only 8
rooms there are 8x6 = 48  different floors!!  Each floor is essentially a different room since
you can?t necessarily get to
something just by being in the
same room as it is.
Now the fun begins. You
can tantalize your party by putting a chest of pearls on the
ceiling, and they have to figure
out how to maneuver through

the tesseract to turn the ceiling into a floor! Imagine the battles
between parties standing on different walls! Or, how about flights of
arrows coming down from a party on the ceiling that cannot be
reached with swords! The same stairway can be going up or down
depending on the way you are standing on it! Shades of Escher!!
Another interesting effect is that not only is gravity a property of
people, but of possessions as well. Let?s imagine that the adventurers meet a party of monsters in a corner and that the monsters are
standing on a different wall. Let?s say that the monsters are defeated
and the leader has a magic sword. Thandatir picks up the sword from
the wall and finds that it is unusable, because gravity is pulling it to
the side instead of toward the ground. If he wants to use it, he either
has to get out of the tesseract or have some of the party guard it while
he races around the tesseract (trying to come into the room so that
down for him is the same as down for the sword)?and we all know
that splitting the party is a risky proposition in any event.

Of course, the party could use this to their advantage. Let?s say
that Thanatos boosts Terah up on his shoulders. Terah grabs hold of
a chair on the ceiling that weighs less than he does and pulls it down
to his ?floor.? This chair could then be used as a ?balloon? by tying it
to a heavy chest and having the weight of the chair pulling up
balance some of the weight of the chest pulling down.
The next problem for the DM is an architectural one. Obviously,
the rooms have to be cubical, but where should doors, stairs, and
ladders be, and how big should the rooms be?

The major consideration is as follows. You need to have good
connectivity. Since you presumably want your party to have access
to every wall as a floor (although maybe you do not. . .) you might
want a stairway or ladder to the ceiling, doors on all walls, and a
trap-door on every ceiling and floor. Note that you have to be able to
get up and down somewhere, otherwise you will never be able to
turn a ceiling into a wall. Also note that if you want complete
connectivity, this means a ladder or stairway from  every  floor to the
appropriate ceiling. As far as I can see, there are three answers.
The first possibility is to have small rooms (about 8?x8?x8?), so
that you can climb through any trap door in the ceiling and then
safely drop to the floor of the room below. Unfortunately, such
rooms are little more than closets.

The second possibility is to have large rooms (20?x20?x20? and
up) and have 4 doors in each wall, one on each side (fig 5A). In the
center of each floor you have a spiral stairway/elevator/ladder/
whatever for going up and down.

The third, and to me the most interesting, possibility is to have
large rooms and only one square door in the center of each wall. You
have a stairway leading down from every door to the door of every
adjacent ?floor.? If Norman wants to get to the next room, he climbs a
flight of stairs to the door, goes through, and climbs down another
flight of stairs to the floor. Note that each stairway can be used by
people in two different orientations just like in Escher?s Relativity.
But how does Norman go up or down? There are two possibilities.
The easiest is that he climbs up to the door in the middle of a wall

(any wall), then  he climbs onto the back  of the  stairway leading from
that wall to the ceiling  (fig 5B). If the stairway is just a flight of steps in
the air, the back of the stairway is another stairway! When he gets to
the ceiling, he climbs back around and goes through the door in the
ceiling (presumably there is a platform provided for this). Another,
more complicated, way is to have tubes rather than plain stairways
leading from door to door, then have another stairway functioning
as the ?ceiling? of each stairway (fig 5C). This may be less esthetic,
but it allows more battles within stairways.

The last problem is, how do you get in and out of the tesseract?
Mathematically, this is no problem at all, since each cube of the
tesseract borders on the outside as well as on other cubes just like the
faces of a cube border on the outside as well as other faces of the
cube. In reality, there are other considerations. People are not
4-dimensional, so presumably they can go one and only one way
through every door. Getting the party in is no problem, but how
should they get out? If they are very high-level, you may make them
rely on a  Wish  or a  Teleport.  For lower-level parties you might want
to have magical helms or rings that will take you out to the real world
if you leave the right door with the right orientation, or perhaps you
might want something as pedestrian as a lever on the wall. Whatever
it is, you probably want the exit to be a different door than the
entrance (or at least in a different orientation; you don?t want to
make things too easy), but you should somehow mark it, or have a
map to it, or have some of the monsters tell where it is if they are
questioned and suitably paid, because there are 48 different doors
with 6 different orientations for each (up and down count, too!)
which amounts to 288 different possibilities!

To all you fellow dungeon masters, have fun! I?m planning to. To
all you intrepid adventurers, beware! Go read Heinlein's "And He
Built A Crooked House" and get a copy of Escher?s Relativity,
because you never know when your DM may have things other than
Carrion Crawlers attacking from the ceiling.