-	-	-	-	-
Dragon	-	-	-	Dragon 49

The many and varied worlds of the D&D® and AD&D™ universes typically have one feature in common: They are flat. In
fact, they are a good deal flatter than a well-educated medieval
would have conceived ours. Not unreasonably, players map
their diverse journeys through this landscape on two-dimensional paper, making no allowance for curvature. One can
excuse the matter easily enough by claiming the world is so vast
that curvature is not apparent unless many thousands of miles
are traversed, or that the referee’s maps represent polyconic
projections of a spherical planet.

There are alternatives, however. The intrepid designer will not
balk at creating a spherical world, but there is no real need for
the world to be literally spherical in shape. Polyhedral solids can
effectively simulate spheres and are easier than spheres to
translate into a hexagonal pattern for mapping purposes.

A cylinder is the simplest three-dimensional world, and most
“conventional” D&D worlds can quickly be adapted to this form.
Merely design a flat, rectangular world with opposing edges in
register. Such a structure can be infinite in surface area, or finite
and capped with circular areas of an appropriate diameter. The
referee should keep an eye on the change of seasons based on
the inclination of the axis, orbital eccentricity, orbits of multiple
suns, and other factors.

Cylinders can exhibit unique complications. Inverted (hollow) cylinders create a Pellucidar-like effect, and small ones
could easily be space colonies.

One can design flat worlds with both pairs of opposing edges
in register. Such a system is two different cylinders simultaneously. A party that ventures “off” the south edge reappears at a
corresponding point on the north edge, while those who wander
across the east limit reappear in the west, It is as if the world cylinder were alternately glued together along different sides.
Players can circumnavigate any of these systems and become
disoriented unless they chance upon some feature that reveals
the pattern.

Any polygonal world can be converted so that its edges are in
exact registration. Hexagonal worlds can then be “glued together” in three parts. One can further distort matters by randomly connecting any two of the six sides as characters pass the
boundary of one edge.

Other patterns such as octagonal, triangular, and even irregular polygons are adaptable to this sort of trick. To complicate
things one step more, use a randomization scheme that is not
equally probable for all edges. For those who don’t wish to be
tied down to three dimensions, be sure to include edges that
connect with other worlds, planes of existence, or time periods.

The inventive reader has no doubt already seen the logical
continuation of this kind of world-building. Instead of capping a
cylinder with circles, use hexagons. The hex-grid fits better on
this type of prism, The next most obvious shape might be a cube,
but a better approximation of a sphere is the regular icosahedron. This 20-sided structure made up of equilateral triangles is
familiar to all D&D players and DMs as the shape of a 20-sided
die.

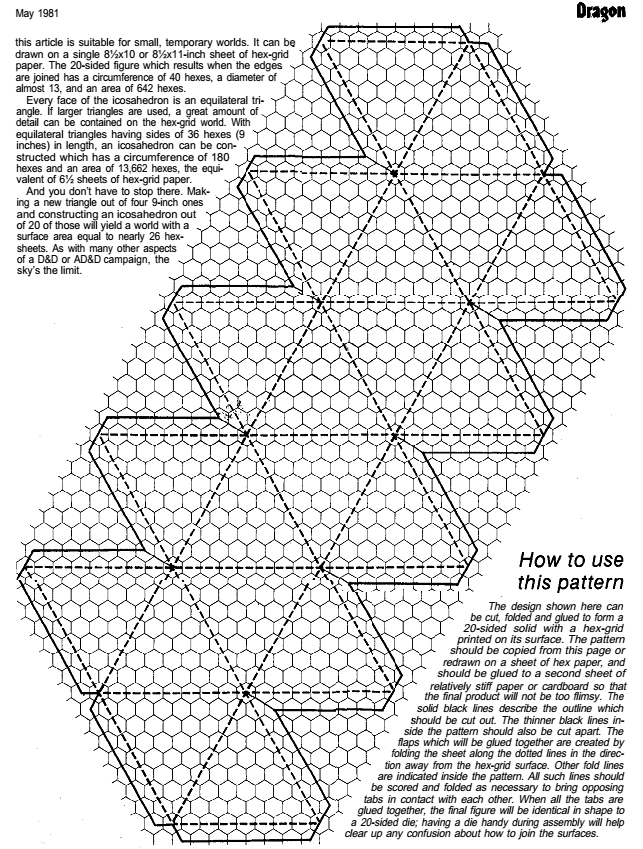
A two-dimensional pattern that may be drawn on a hex-grid
and then cut, folded and glued to form an icosahedron with a
grid already on it is shown in the accompanying illustration.
When placing terrain on this pattern, be sure that sides adjacent
to each other in the finished three-dimensional structure are
properly in register.

Do not create coastlines, rivers, mountain ranges, and other
features which end abruptly without reason. When the pattern in
the illustration is reproduced and assembled, there are 20 faces,
12 vertices and 30 edges. Note that five edges join at the north
pole and another five at the south pole. These are termed “polar
edges” for convenience in discussing their unusual properties.

The hex-pattern fits all faces and most edges without difficulty, but matters are more complicated when one examines the
hex-grid at the vertices and polar edges.

First, observe that vertices are formed at the junction of five
triangular faces and are actually pentagons. Vertices are tricky
because of their unusual pattern of directions. Compare a
standard hex on any face with a vertex other than a pole. The
typical hex has edges that face northeast, east, southeast,
southwest, west and northwest. A vertex in the southern hemisphere lacks sides that “point” southeast and southwest but has
true south. A northern-hemisphere vertex lacks the directions of
northeast and northwest but has north as a hex-side. Any party
that ventures to the precise north or south pole will become
disoriented due to the absence of all directions except south or
north, respectively. The unfortunate members of such a party
will have five choices of the same compass heading.

Directions are a bit muddled at the hexes lying on polar edges.
In the north the directions of the hex-sides are north, east,
southeast, south, southwest and west. Hex-side directions in
the southern hemisphere are north, northeast, east, south, west
and northwest.

Any party that travels around one or more vertices will experience distance distortion due to curvature of the world. The
effect is graphically caused by crossing a polar edge and is most
dramatic when the party concerned treads near a pole and then
returns by an equatorial route. As long as a group of adventurers
travels on the full hexes of the pattern illustrated on the opposite
page, there is no difficulty. But when one of the, “gaps” is
crossed, terrain is no longer mappable in two dimensions.

The referee, as always, has the option to make things simple
or complex. A continent can be laid out so that it conforms to the
flat pattern, with polar edges located at sea or in forbidding
terrain. Players will have little difficulty.
 

On the other hand, land masses can be centered on polar
edges and roads designed to lead the unwary astray. Rivers,
lakes, shorelines, mountain passes, and other natural means of
passage can repeatedly cross polar edges, compounding the
disorientation.
 

A small-diameter world will puzzle players who unwittingly
circumnavigate it no matter how they proceed. Large-diameter
worlds require considerable time and effort to circle, but they
cause a greater distortion when characters attempt to force the
terrain onto a flat map.

Since a typical hex has six cardinal points, most players will
call their direction of travel in terms of northeast, east,
southeast, southwest, west and northwest. If they happen to be
on an edge or vertex where the direction called does not exist as
a hex-side, the referee should randomly select one of the two
directions that bracket the one specified but not available. Poles
require randomization of five directions, unless the party is
using some landmark, like a range of mountains on the horizon,
to orient itself. Some enterprising characters have managed to
devise clever means of celestial navigation. Moderately highlevel spells will also aid in orientation if properly employed.

Needless to say, any polyhedron can be used as the basis of a
world, especially those with triangular, square, or hexagonal
faces. Regular tetrahedra (four-sided dice) and octahedra
(eight-sided dice) make fine world models. Moons, asteroids
and planetoids can be built using irregular polyhedra, limited
only by the imagination of the designer. To the dedicated Dungeon Master, even polyhedral Klein’s Bottles are possible.

The pattern for a small icosahedron which is reproduced with
this article is suitable for small, temporary worlds. It can be
drawn on a single 8½x10 or 8½x11-inch sheet of hex-grid
paper. The 20-sided figure which results when the edges
are joined has a circumference of 40 hexes, a diameter of
almost 13, and an area of 642 hexes.

Every face of the icosahedron is an equilateral triangle. If larger triangles are used, a great amount of
detail can be contained on the hex-grid world. With
equilateral triangles having sides of 36 hexes (9
inches) in length, an icosahedron can be constructed which has a circumference of 180
hexes and an area of 13,662 hexes, the equivalent of 6½ sheets of hex-grid paper.

And you don’t have to stop there. Making a new triangle out of four 9-inch ones
and constructing an icosahedron out
of 20 of those will yield a world with a
surface area equal to nearly 26 hexsheets. As with many other aspects
of a D&D or AD&D campaign, the
sky’s the limit.